Answer:
The two possible distance are 147.5km and 64.4km
Explanation:
Given
See Attachment for Illustration
Required
Determine the possible distance of ship A from the boat
The distress is represented by X;
So, the question requires we calculate distance AX;
This will be done using cosine formula as follows;
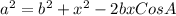
In this case;
a = 70;
b = ??
x = 120
A = 28 degrees
Substitute these values in the formula above
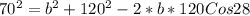
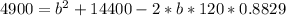
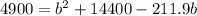
Subtract 4900 from both sides
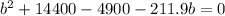
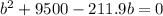
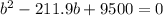
Solve using quadratic formula
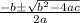
Substitute 1 for a; -211.9 for b and 9500 for c
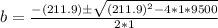
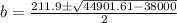
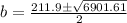

This can be splitted to
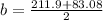 or
or
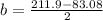
 or
or
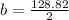
 or
or
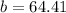
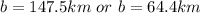
Hence, the two possible distance are 147.5km and 64.4km