Question

The fourth term of an arithmetic

progression is one less than twice the
second term - If the sixth term is 7
find the first term​

Answer 1

`\huge{ \underline{ \underline{ \bf{ \orange{Solution:}}}}}`

Let the first term of the AP be a and the common difference of the AP be d

We know the formula for finding the nth term,

`\large{ \boxed{ \rm{a_n = a + (n - 1)d}}}`

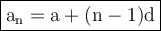
Here,

• an = nth term of the AP
• n = number of terms of AP

By using formula,

• a4 = a + 3d
• a2 = a + d
• a6 = a + 5d

According to given condition,

⇛ a4 = 2a2 - 1

⇛ a + 3d = 2(a + d) - 1

⇛ a + 3d = 2a + 2d - 1

⇛ a - 2a + 3d - 2d = -1

⇛ -a + d = -1

⇛ a - d = 1

Then,

⇛ a = d + 1-----------(1)

It is given that, a6 = 7

⇛ a + 5d = 7

Putting a from eq.(1),

⇛ d + 1 + 5d = 7

⇛ 6d + 1 = 7

⇛ 6d = 6

⇛ d = 6/6 = 1

Putting value of d in eq.(1),

⇛ a = 1 + 1 = 2

⛈ First term of the AP(a) = 2

━━━━━━━━━━━━━━━━━━━━