Let the first term of the AP be a and the common difference of the AP be d
We know the formula for finding the nth term,
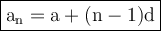
Here,
- an = nth term of the AP
- n = number of terms of AP
By using formula,
- a4 = a + 3d
- a2 = a + d
- a6 = a + 5d
According to given condition,
⇛ a4 = 2a2 - 1
⇛ a + 3d = 2(a + d) - 1
⇛ a + 3d = 2a + 2d - 1
⇛ a - 2a + 3d - 2d = -1
⇛ -a + d = -1
⇛ a - d = 1
Then,
⇛ a = d + 1-----------(1)
It is given that, a6 = 7
⇛ a + 5d = 7
Putting a from eq.(1),
⇛ d + 1 + 5d = 7
⇛ 6d + 1 = 7
⇛ 6d = 6
⇛ d = 6/6 = 1
Putting value of d in eq.(1),
⇛ a = 1 + 1 = 2
⛈ First term of the AP(a) = 2
━━━━━━━━━━━━━━━━━━━━