Answer:

Explanation:
We want to solve the quadratic inequality:
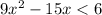
In order to solve a quadratic inequality, find its zeros. That is, let the inequality sign be an equal sign and solve for x. We do this because it denotes when the graph crosses the x-axis: that is, when it is positive and/or negative. This yields:
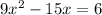
Solve for x:
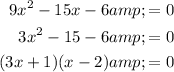
By the Zero Product Property:
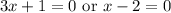
Hence:
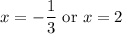
Now, we can test intervals. The three intervals are: all values less than -1/3, values between -1/3 and 2, and all values greater than 2.
To test the first interval, let x = -1. Substitute this into our original inequality:
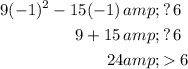
The resulting symbol is "greater than," which is not our desired symbol.
To test the interval between -1/3 and 2, we can let x = 0:
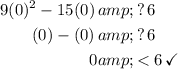
The resulting symbol is indeed less than. So, the interval (-1/3, 2) is a part of our solution.
Finally, to test the third interval, let x = 3. Then:
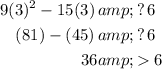
Again, this is not our desired symbol.
In conclusion, our only solution is the interval:
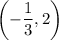
Or as an inequality:
