Question

P and Q have coordinates (-2,3) and (5,4) respectively. Reflect P inthe X-axis to P' and Q in tha Y-axis to Q' .Find the distance between P'Q'.​

Answer 1

Explanation:

Hey, there!!

Let's simply work with it,

The given coordinates are, P(-2,3) and Q(5,4).

Now, finding the P' and Q'.

Reflection on x- axis .

P(x,y)---------> P' (x,-y)

P (-2,3)----------> P'(-2,-3)

Now, let's find Q'

Reflection on y-axis.

Q(x,y)----------> Q'(-x,y)

Q(5,4)---------> Q'(-5,4)

Now, The points are P'(-2,-3) and Q'(-5,4)

By distance formulae,

`P'Q' = \sqrt{( {x2 - x1)}^(2) + ( {y2 - y1)}^(2) }`

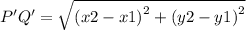
Putting their values,

`P'Q' = \sqrt{( { - 5 + 2)}^(2)( {4 + 3)}^(2) }`

`P'Q' = \sqrt{( { - 3)}^(2) + ( {7)}^(2) }`

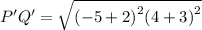
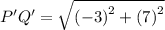
Simplifying them we get,

`pq = √(58)`

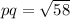
Therefore, the distance between P'and Q' is root under 58 units.

Hope it helps...