Question

Answer each question.

1. Determine the type of graph for each function.
a. f(x) = 3x + 1
b. f(x) = x - 6x + 5
c. f(x) = 4x - x + 1

Need help with these Linear or Quadratic functions

Answer 1

Explanation:

a- f(x)=3x+1 it is linear equation

b: f(x)=x-6x+5

f(x)=-5x+5 linear equation

c: f(x)=4x-x+1

f(x)=3x+1 (linear equation)

(if there is no exponent then the graph is linear)

Answer 2

A: Linear

B: Linear

C: Linear

Explanation:

So we have three functions:

`f(x)=3x+1\\f(x)=x-6x+5\\f(x)=4x-x+1`

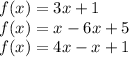
To determine the type of graph for each function, simplify each of them and then we can determine whether it's linear or quadratic.

1)

We have:

`f(x)=3x+1`

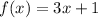
This has a degree of 1. Quadratics have a degree of 2. In other words, quadratics have a x^2 term. There isn't one here, so this is a linear equation.

2)

We have:

`f(x)=x-6x+5`

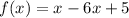
Simplify:

`f(x)=-5x+5`

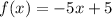
Again, this is of degree 1. There is no x^2 term. Thus, this is also a linear equation.

3)

We have:

`f(x)=4x-x+1`

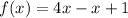
Simplify:

`f(x)=3x+1`

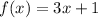
This has a degree of 1. There is no x^2 term. Thus, this is also a linear equation.