Answer:

Given:
Velocity (u) = 20 m/s
Acceleration due to gravity (g) = 10
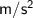
To Find:
Time (t) being in which body remains in air.
Step-by-step explanation:
Formula:
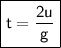
Substituting values of u & g in the equation:
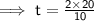
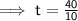
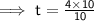
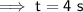

Time (t) being in which body remains in air = 4 seconds