Question

What is the maximum speed with which a 1200-kg car can round a turn of radius 90.0 m on a flat road if the coefficient of static friction between tires and road is 0.70?

2. Is this result independent of the mass of the car?

Answer 1

The value is
`v = 24.85 \ m/s`

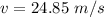
Yes

Step-by-step explanation:

From the question we are told that

The mass of the car is
`m= 1200 \ kg`

The radius is
`r = 90 \ m`

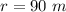
The coefficient of static friction is
`\mu_s = 0.70`

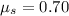
Generally at maximum speed the centripetal force acting on the car is equal to the friction force on the car

So

`F_c = F_f`

`(m v^2)/(r) = \mu_s * m * g`

=>
`v = √(\mu_s * g * r )`

=>
`v = √( 0.70 * 9.8 * 90 )`

=>
`v = 24.85 \ m/s`

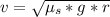
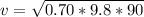
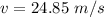
Yes the value is independent of the mass because from the equation above we see that v is independent of mass

Answer 2

78.6m/s

Step-by-step explanation:

We know that frictional force also contributes to the centripetal force that keeps the car in circular motion in the turn

And is given as

F= mv²/r

But the frictional force is

F= ugm

= = 0.7*1200*9.8= 8232N

To find maximum velocity v we say

V= √F x r/m

= √ 8232* 90 /1200

= 78.6m/s

2. Yes it is independent of mass of car