Question

The measures of the sides of a triangle are 20 24 and 30. Find the measures of the segments former where the bisector of the smallest angle meets the opposite side.

Answer 1

One segment is 8.89 long and the other one is: 11.11 long

Explanation:

Recall that the bisector of a triangle divides the opposite side it intersects into two segments that are proportional to the other two sides of the triangle.

In our case the bisector is generated on the angle opposite to the size 20 side (it is the smallest angle in the triangle since it is opposite to the smallest side). This bisector divides the side of length 20 into a segment of length x and a segment of length 20-x.

The proportionality indicated by the bisector theorem gives;

`(20-x)/(x) =(30)/(24)`

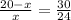
and we can solve for "x":

`(20-x)/(x) =(30)/(24)\\24\,(20-x)=30\,x\\480-24\,x=30\,x\\480=54\,x\\x=480/54\\x\approx8.89`

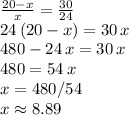
Then the other segment is: 20 - 8.89 = 11.11