Question

slader The logarithmic equation is a nonlinear regression equation of the form ya. The accompanying data are the shoe sizes and heights​ (in inches) of men. Graphs of the regression line and the logarithmic equation are also provided. Which equation is a better model for the​ data? Explain.

Answer 1

The graphs and the table is missing in the question.

Step-by-step explanation:

The guidelines for interpreting correlation co-efficient r are :

1. Strong correlation 0.7<|r|≤1

2. Moderate correlation 0.4<|r|<0.7

3. Weak correlation 0.2<|r|<0.4

4. No correlation 0≤|r|<0.2

Logarithmic regression

(i). Mean :
`$ {\overset{-}{ln}x} = (\sum ln x_i)/(n), \ \ \ {\overset{-}y} = (\sum y_i)/(n) $`

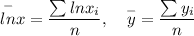
(ii) Trend line :
`$ y = A +B \ln x, \ \ B = (S_(xy))/(S_(xx)), \ \ A={\overset{-}y-B{\overset{-}{\ln x}}}$`

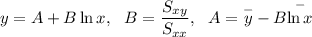
(iii). Correlation coefficient :
`$ r = \frac {S_(xy)}{\sqrt{S_(xx)} \sqrt{S_(yy)}} $`

`$ S_(xx) = \sum (\ln x_i - {\overset{-}{\ln x}})^2 = \sum (\ln x_i)^2-n. ({\overset{-}{\ln x}})^2$`

`$ S_(yy) = \sum(y_i - {\overset{-}y})^2 = \sumy_i^2 - n. {\overset{-}y^2}$`

`$ S_(xy) = \sum(\ln x_i - {\overset{-}{\ln x}})(y_i-{\overset{-}y}) = \sum \ln x_i y_i - n. {\overset{-}{\ln x}}{\overset{-}y} $`

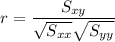
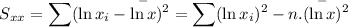
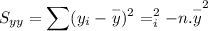
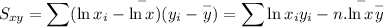
Now using the technology we can calculate

The equation of the regression curve is y = A + B(lnx)

we get A = 30.72 , B = 17.19

The equation of regression curve is
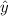`$ \hat y$` = 30.72 + 17.19(lnx)