Answer:
The graphs and the table is missing in the question.
Step-by-step explanation:
The guidelines for interpreting correlation co-efficient r are :
1. Strong correlation 0.7<|r|≤1
2. Moderate correlation 0.4<|r|<0.7
3. Weak correlation 0.2<|r|<0.4
4. No correlation 0≤|r|<0.2
Logarithmic regression
(i). Mean :
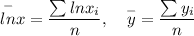
(ii) Trend line :

(iii). Correlation coefficient :
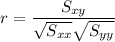

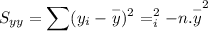
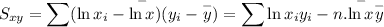
Now using the technology we can calculate
The equation of the regression curve is y = A + B(lnx)
we get A = 30.72 , B = 17.19
The equation of regression curve is
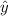 = 30.72 + 17.19(lnx)
= 30.72 + 17.19(lnx)