Question

The sum of two numbers is 15, and their product is 16. What is the sum of the reciprocals of the two numbers? Express your answer as a common fraction.

Answer 1

The sum of the reciprocal of two numbers are

`(1)/(x) + (1)/(y)= (15)/(16)`

Explanation:

Step(i):-

Let x , y are two numbers

Given data the sum of two numbers = 15

x + y = 15 ...(i)

The product of two numbers = 16

x y = 16 ...(ii)

we know that

(x-y)² = (x + y)² - 4 x y

= (15)²- 4(16)

= 225 - 64

= 161

x-y = 12.68 ≅13 ...(iii)

Step(ii):-

We have

x + y = 15 ...(a)

x -y = 13 ...(b)

Solving (a) and (b)

2x = 27.68

x = 13.84

Substitute x = 13.84 in equation (i)

x + y = 15

13.84 + y = 15

y = 15 - 13.84

y = 1.16

Step(iii):-

The positive numbers are x = 13.84 and y = 1.16

The sum of the reciprocal of two numbers are

`(1)/(x) + (1)/(y) = (1)/(13.84) + (1)/(1.16)`

=
`(15)/(16)`

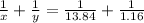
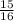
Conclusion:-

The sum of the reciprocal of two numbers are

`(1)/(x) + (1)/(y)= (15)/(16)`