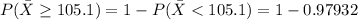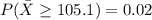Question

New heat lamps are reported to have the mean lifespan of 100 hours with a standard deviation of 15 hours. Before replacing their current lamp to the new heat lamps for the university, OSU decided to test whether the mean lifetime is equal to 100 or not by sampling 36 heat lamps. They turned them on and recorded the time, in hours, until each lamp failed. The sample provided a mean lifespan is 105.1 hours.

1) What set of hypotheses are correct for this problem?
SET 1 - H0: µ = 100 hours , Ha: µ < 100 hours
SET 2 - H0: µ = 100 hours , Ha: µ > 100 hours
SET 3 - H0: µ = 100 hours , Ha: µ ≠ 100 hours
A) SET 1.
B) SET 2.
C) SET 3.
2) If we assume the null hypothesis to be true, the average of the distribution of sample means, μ x ¯, from a sample size of 36 is:______.
a) 15.
b) 115.
c) 100.
d) 105.1. .
3) According to the Central Limit Theorem, the standard deviation of the distribution of the sample means is:______.
a) 115.
b) 15.
c) 6.
d) 2.5. .
4) What is the approximate probability of observing a sample mean of 105.1 or more from the distribution of sample means, again assuming that the null hypothesis is true?
a) 0.68.
b) 0.025.
c) 0.975.
d) 0.16.

Answer 1

1

The correct option is C

2

The correct option is C

3

The correct option is A

4

The correct option is B

Explanation:

From the question we are told that

The population mean is
`\mu = 100`

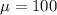
The standard deviation is
`\sigma = 15`

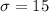
The sample size is
`n = 36`

The sample mean is
`\= x = 105.1`

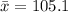
Generally

The null hypothesis is
`H_o: \mu = 100 \ hours`

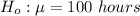
The alternative hypothesis is
`H_a : \mu \\e 100\ hours`

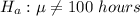
Given that the null hypothesis is true then the distribution of sample means
`\mu_(\= x )`, from a sample size of 36 is mathematically represented as

`\mu_(\= x ) = \mu`

=>
`\mu_(\= x ) = 100`

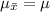
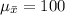
According to the Central Limit Theorem the test stated in the question is approximately normally distributed if the sample size is sufficiently large
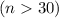`(n > 30 )` so given that the sample size is large n = 36

Then the test is normally distributed and hence the standard deviation is 15

Generally the standard error of mean is mathematically represented as

`\sigma_(\= x ) = ( \sigma )/(√(n) )`

=>
`\sigma_(\= x ) = (15)/(√(36) )`

=>
`\sigma_(\= x ) = 2.5`

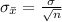
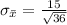
Generally the approximate probability of observing a sample mean of 105.1 or more is mathematically represented as

`P( \= X \ge 105.1 ) =1 - P(\= X < 105.1) = 1- P((\= X - \mu )/(\sigma_(\= x )) <(105.1 - 100)/(2.5) )`

=>
`P( \= X \ge 105.1 ) =1 - P(\= X < 105.1) = 1- P(Z<2.04 )`

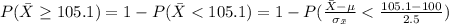
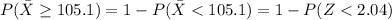
From the z-table (reference calculator dot net )

`P(Z<2.04 ) = 0.97932`

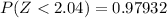
So

`P( \= X \ge 105.1 )= 1 - P(\= X < 105.1) = 1- 0.97932`

`P( \= X \ge 105.1 ) =0.02`