Question

Kristin is building a pattern using triangles. The table shows the number of triangles in the first 4 terms of the pattern.

Term Number (7)
1 2 3 4
Number of Triangles (t) 1 3 5 7
Which formula describes the number of triangles in the nth term of the pattern?
O A n=1+2
O B. n=1+3
Oc. n = 21-1
OD n = 2t + 3

Answer 1

an = 2t -1

Explanation:

We are adding 2 each time

1+2 =3

3+2 = 5

5+2 = 7

an is the nth term in the sequence and t is the number of triangle

an =1+ 2(t-1)

Distribute

an = 1 +2t -2

an = 2t -1

Answer 2

`\bold{n =2t-1}`

Explanation:

Given table is:

`\begin{center}\begin{tabular}{ c c}Term Number (t) & Number of triangles (n) \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \\\end{tabular}\end{center}`

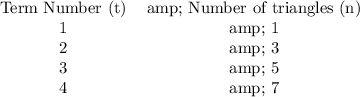
i.e. when term number, t = 1, number of triangles (n) = 1

when term number, t = 2, number of triangles (n) = 3

when term number, t = 3, number of triangles (n) = 5

when term number, t = 4, number of triangles (n) = 7

If we closely look at the pattern, number of triangles (n) in each row are 1 lesser than twice of term number (t).

i.e. for
`t=1, n = 2* 1 -1=1`

`t=2, n = 2* 2 -1=3`

`t=3, n = 2* 3 -1=5`

`t=4, n = 2* 4 -1=7`

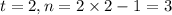
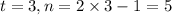
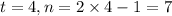
Therefore, the number of triangles in the nth term will be given as:

`\bold{n =2t-1}`