Answer:
Values of k can be 0, 1, or 2 such that intersection of the given lines lie in the 1st quadrant.
Explanation:
Given two lines:
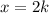 and
and
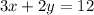
To find:
Values of 'k' such that the intersection of given two lines lie in the first quadrant.
Solution:
In 1st quadrant, the values of
 and
and
 both are positive.
both are positive.
So, let us find out intersection of the two lines.
Intersection of the two lines can be found by solving the two equations for the values of
 and
and
 .
.
Given that
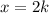 to be in the first quadrant, the value of k must be positive.
to be in the first quadrant, the value of k must be positive.
Let us put
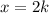 in the equation
in the equation
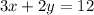 to find the intersection point.
to find the intersection point.
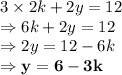
For y to be positive:
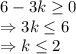
So, values of k can be 0, 1, or 2 such that intersection of the given lines lie in the 1st quadrant.