Question

A medical researcher wants to compare the pulse rates of smokers and non-smokers. He believes that the pulse rate for smokers and non-smokers is different and wants to test this claim at the 0.01 level of significance. A sample of 75 smokers has a mean pulse rate of 76, and a sample of 73 non-smokers has a mean pulse rate of 72. The population standard deviation of the pulse rates is known to be 9 for smokers and 10 for non-smokers. Let µ1 be the true mean pulse rate for smokers and µ2 be the true mean pulse rate for non-smokers.

Step 1 of 5: State the null and alternative hypotheses for the test.
Step 2 of 5: Compute the value of the test statistic. Round your answer to two decimal places.
Step 3 of 5: Find the p-value associated with the test statistic. Round your answer to four decimal places.
Step 4 of 5: Make the decision for the hypothesis test.
Step 5 of 5: State the conclusion of the hypothesis test.

Answer 1

We conclude that the pulse rate for smokers and non-smokers is equal.

Explanation:

We are given that a medical researcher wants to compare the pulse rates of smokers and non-smokers.

A sample of 75 smokers has a mean pulse rate of 76, and a sample of 73 non-smokers has a mean pulse rate of 72. The population standard deviation of the pulse rates is known to be 9 for smokers and 10 for non-smokers.

Let
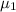`\mu_1` = true mean pulse rate for smokers

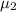`\mu_2` = true mean pulse rate for non-smokers

So, Null Hypothesis,
`H_0` :
`\mu_1=\mu_2` {means that the pulse rate for smokers and non-smokers is same}

Alternate Hypothesis,
`H_A` :
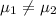`\mu_1\\eq \mu_2` {means that the pulse rate for smokers and non-smokers is different}

The test statistics that will be used here is Two-sample z-test statistics because we know about the population standard deviations;

T.S. =
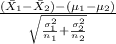`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{\sqrt{(\sigma_1^(2) )/(n_1)+(\sigma_2^(2) )/(n_2)} }` ~ N(0,1)

where,
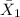`\bar X_1` = sample mean pulse rate of smokers = 76

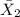`\bar X_2` = sample mean pulse rate of non-smokers = 72

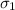`\sigma_1` = population standard deviation of the pulse rates of smokers = 9

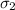`\sigma_2` = population standard deviation of the pulse rates of non-smokers = 10

`n_1` = sample of smokers = 75

= sample of smokers = 73

So, the test statistics =
`\frac{(76-72)-(0)}{\sqrt{(9^(2) )/(75)+(10^(2) )/(73)} }`

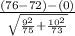
= 2.56

The value of the z-test statistics is 2.56.

Also, the P-value of the test statistics is given by;

P-value = P(Z > 2.56) = 1 - P(Z
`\leq` 2.56)

= 1 - 0.9948 = 0.0052

For the two-tailed test, the P-value is calculated as = 2
`*` 0.0052 = 0.0104.

Now, at a 0.01 level of significance, the z table gives a critical value of -2.58 and 2.58 for the two-tailed test.

Since the value of our test statistics lies within the range of critical values of z, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the pulse rate for smokers and non-smokers is equal.