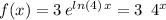Answer:
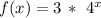
Explanation:
to find the equation of an exponential function, just points on the function's graph are needed.
Recall that the exponential function has a general expression given by:
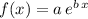
so we impose the condition for the function going through the first point (0,3) as:
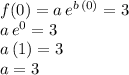
Now,knowing the parameter a, we can find the parameter b using the other point:
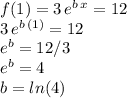
Therefore, the function can be written as: