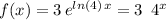Question

The points (0,3) and (1,12) are solutions of an exponential function. What is the equation of the exponential function?

Answer 1

C)

h(x) = 3(4)x

Answer 2

`f(x) =3\,*\,\,4^x`

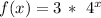
Explanation:

to find the equation of an exponential function, just points on the function's graph are needed.

Recall that the exponential function has a general expression given by:

`f(x) = a \,e^(b\,x)`

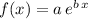
so we impose the condition for the function going through the first point (0,3) as:

`f(0) = a \,e^(b\,(0))= 3\\a\,e^0=3\\a\,(1)=3\\a = 3`

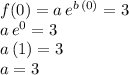
Now,knowing the parameter a, we can find the parameter b using the other point:

`f(1) = 3 \,e^(b\,x)= 12\\3\,e^(b\,(1))=12\\e^b=12/3\\e^b=4\\b=ln(4)`

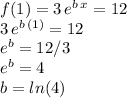
Therefore, the function can be written as:

`f(x) = 3 \,e^(ln(4)\,x)=3\,\,\,4^x`