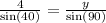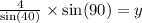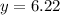Answer:
y = 6.22
You can solve this in two ways.
1.) Use SOH CAH TOA:
I typically start off by labeling the sides of the triangle with H (hypotenuse), O (opposite), and A (adjacent). Because I need to figure out what y is when given an angle and 4, I will use CAH, or cosine.
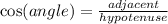
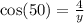
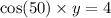
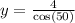
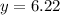
2.) Use Law of Sines:
Solve for the last angle inside the triangle first.
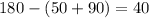
Then use the angle you found (40°) in the equation.