Answer:
Speed of plane in still air = 780 km/h
Speed of air = 52 km/hr
Explanation:
Let the speed of plane in still air = u km/h
Let the speed of air = v km/h
Against the air, the resultant speed = (u-v) km/hr
With the air, the resultant speed = (u+v) km/hr
Formula for speed is given as:

Given that:
Distance = 5824 km
Time taken against the wind = 8 hours
Speed against the wind:
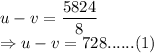
Time taken with the wind = 7 hours
Speed with the wind:
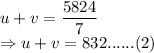
Adding (1) and (2):
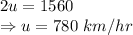
By equation (1):

Speed of plane in still air = 780 km/h
Speed of air = 52 km/hr