Question

Last math hw question

Answer 1

(a) -5, 4

(b) no solution

Explanation:

(a) x+5 will be zero when x = -5.

x-4 will be zero when x = 4.

The restricted values are: x = -5 and x = 4.

__

(b) We can simplify the difference of the two sides of the equation.

`(4)/(x+5)+(5)/(x-4)=(45)/((x+5)(x-4))\\\\(4(x-4)+5(x+5))/((x+5)(x-4))=(45)/((x+5)(x-4))\\\\(9x+9)/((x+5)(x-4))-(45)/((x+5)(x-4))=0\\\\(9(x-4))/((x+5)(x-4))=0\\\\(9)/(x+5)=0\qquad\text{NO SOLUTION}`

__

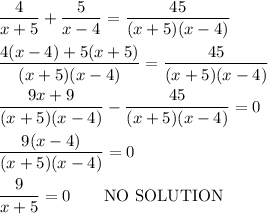
The graph shows there are no values of x that cause the two sides of the equation to be equal (their difference to be zero).