Hello, a car was purchased for $20,000.
This is the initial value.
The car depreciates by 22% of each year.
After 1 year, the value is the initial value 20,000 minus 22% of 20,000.
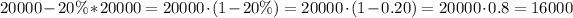
After 2 years, the value is.
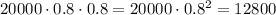
Let's take n a positive integer, after n years, the value is.
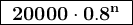
a) After 12 years, the value is.
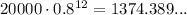
This is rounded to $1,374
b) We need to find n such that
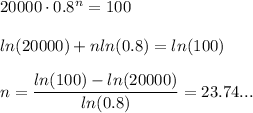
This is around 23.75 meaning 23 years and 75% of 1 year (meaning 9 months).
So to be worth less than $100, 23 years and 9 months are required.
Thank you