Question

A wind turbine rotates at 20 rev/min. If its power output is 2.0 MW, the torque produced on the turbine from the wind is

Answer 1

The torque torque produced on the turbine from the wind is approximately 955 kN·m

Step-by-step explanation:

The number of revolution per minute of the turbine = 20 rev/min

The power output of the turbine = 2.0 MW

The power transmitted to a shaft equation is given as follows;

`Power , \ P = (2 \cdot \pi \cdot N \cdot T)/(60)`

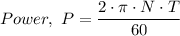
Where;

P = The power transmitted to a turbine shaft = 2.0 MW

N = The number or revolutions per minute = 20 rev/min

T = The torque produced on the turbine by the wind

Therefore;

`Torque , \ T = (P \cdot 60)/(2 \cdot \pi \cdot N ) = (2.0 * 60)/(2 * \pi * 20) = (3)/(\pi ) \ MN \cdot m`

The torque torque produced on the turbine from the wind = 3/π MN·m ≈ 0.955 MN·m = 955 kN·m.