Question

Write the form of the partial fraction decomposition of the function. Do not determine the numerical values of the coefficients. 1/(x-1)(x 9)

Answer 1

`(A)/((x-1)) + (B)/((x-9))`

Explanation:

Given the expression
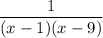`(1)/((x-1)(x-9))`, we are to write the expression as a partial fraction. Writing as a partial fraction means rewriting the expression a s a sum of two or more expression.

Before we will do this we will need to check the nature of the function at the denominator whether it is linear, quadratic or a repeated function. According to the question, the denominator at the denominator is a linear function and since it is a linear function, we can separate both linear function without restriction as shown;

`(1)/((x-1)(x-9)) = (A)/((x-1)) + (B)/((x-9))` where A and B are the unknown constant which are numerical values.