Question

What is the first derivative of r with respect to t (i.e., differentiate r with respect to t)? r = 5/(t2)Note: Use ^ to show exponents in your answer, so for example x2 = x^2. Also, type your equation answer without additional spaces.

Answer 1

The first derivative of
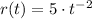`r(t) = 5\cdot t^(-2)` (r(t)=5*t^{-2}) with respect to t is
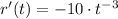`r'(t) = -10\cdot t^(-3)` (r'(t) = -10*t^{-3}).

Explanation:

Let be
`r(t) = (5)/(t^(2))`, which can be rewritten as
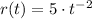`r(t) = 5\cdot t^(-2)`. The rule of differentiation for a potential function multiplied by a constant is:

`(d)/(dt)(c \cdot t^(n)) = n\cdot c \cdot t^(n-1)`,
`\forall \,n\\eq 0`

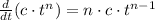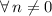
Then,

`r'(t) = (-2)\cdot 5\cdot t^(-3)`

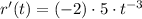
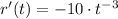`r'(t) = -10\cdot t^(-3)` (r'(t) = -10*t^{-3})

The first derivative of
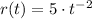`r(t) = 5\cdot t^(-2)` (r(t)=5*t^{-2}) with respect to t is
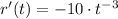`r'(t) = -10\cdot t^(-3)` (r'(t) = -10*t^{-3}).