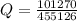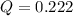Complete Question
You look over the songs in a jukebox and determine that you like 18 of 59 songs.
(a) What is the probability that you like the next four songs that are played? (Assume a song cannot be repeated) Round to three decimal places as needed)
(b) What is the probability that you do not like the next four songs that are played? (Assume a song cannot be repeated.) Round to three decimal places as needed
Answer:
a
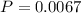
b
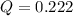
Explanation:
From the question we are told that
The total number of songs is

The number of songs you liked is
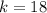
The probability that you like the next four songs that are played? (Assume a song cannot be repeated) is mathematically represented as
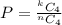
=>
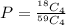
Now using a combination calculator
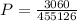
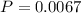
The probability that you do not like the next four songs that are played? (Assume a song cannot be repeated.) is mathematically evaluated as
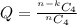
=>

=>

Now using a combination calculator