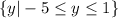Question

Give the domain and range of each relation using set notation​

Answer 1

See below.

Explanation:

First, recall the meanings of the domain and range.

The domain is the span of x-values covered by the graph.

And the range is the span of y-values covered by the graph.

1)

So, we have here an absolute value function.

As we can see, the domain of the function is all real numbers because the graph stretches left and right infinitely. Therefore, the domain of the function is:

`\{x|x\in\textbb{R}\}`

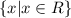
(You are correct!)

For the range, notice how the function stops at y=7. The highest point of the function is (-2,7). There graph doesn't and won't ever reach above y=7. Therefore, the range of the graph is all values less than or equal to 7. In set notation, this is:

`\y`

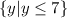
2)

We have here an ellipse.

First, for the domain. We can see the the span of x-values covered by the ellipse is from x=-4 to x=6. In other words, the domain is all values in between these two numbers and including them. Therefore, we can write it as such:

`-4\leq x\leq 6`

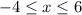
So x is all numbers greater than or equal to -4 but less than or equal to 6. This describes the span of x-values. In set notation, this is:

`\x`

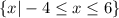
For the range, we can see that the span of x values covered by the ellipse is from y=-5 to y=1. Just like the domain, we can write it like this:

`-5\leq y\leq 1`

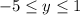
This represents all the y-values between -5 and 1, including -5 and 1.

In set notation, thi is:

`\y`