Answer:
There is no sufficient evidence to support the executive claim
Explanation:
From the question we are told that
The population proportion is
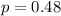
The sample proportion is
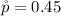
The sample size is
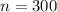
The level of significance is
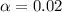
The null hypothesis is
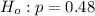
The alternative hypothesis is

Generally the test statistics is mathematically evaluated as

=>
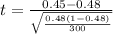
=>

The p-value is mathematically represented as
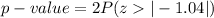
Form the z-table
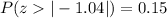
=>
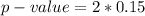
=>
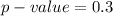
Given that
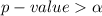 we fail to reject the null hypothesis
we fail to reject the null hypothesis
Hence we can conclude that there is no sufficient evidence to support the executive claim