Answer:
Option (A) and Option (D)
Explanation:
Point on the parabola is (x, y).
Focus given as (2, -4) and directrix of the parabola is y = -6
Therefore, distance of the point from the directrix will be,
d = |(y + 6)|
Similarly, distance of the point (x, y) from the focus will be,
d =
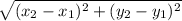
=

Therefore, Option (A) and Option (D) will be the correct options.