Answer:
The difference between the area of the original triangle and the area of the new triangle is
 .
.
Explanation:
The equation for the area of a triangle (
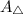 ) is:
) is:
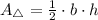
Where:
 - Base, dimensionless.
- Base, dimensionless.
 - Height, dimensionless.
- Height, dimensionless.
The expression for each triangle are described below:
First Triangle (
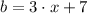 ,
,
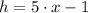 )
)
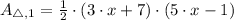
Second Triangle (
 ,
,
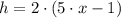 )
)
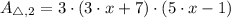
The difference between the area of the original triangle and the area of the new triangle is:
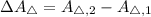
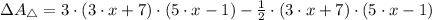

The difference between the area of the original triangle and the area of the new triangle is
 .
.