Question

What are the domain and range of this function y=(x+3)^2 -5

a. domain: (-∞, ∞) range: (-5, ∞)
b. domain: (-∞, ∞) range: (-∞, ∞)
c. domain: (-5, ∞) range: (-5, ∞)
d. domain: (-5, ∞) range (-∞, ∞)

Answer 1

Option A is the correct choice .

Domain will be → all real numbers .

Range will be → y belongs to R : y greater than or equal to -5 .

→ (x+3)^2 It means 0 to infinity

So (x+3)^2-5= (-5, infinity)

→ Range = (-5, infinity )

Answer 2

Answer: Choice A

Note: the range should be
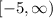`[-5, \infty)`. See explanation below.

===================================================

We can plug in any real number for x to get some output for y. The domain is the set of all real numbers in which we say
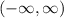`(-\infty, \infty)` which is interval notation. It represents the interval from negative infinity to positive infinity.

The range is the set of possible outputs. The smallest output possible is y = -5 which occurs at the vertex (3,-5). We can get this y value or larger. So we can describe the range as the set of y values such that
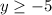`y \ge -5` and that translates to the interval notation
`[-5, \infty)`.

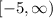The square bracket says "include this endpoint" while the curved parenthesis says to exclude the endpoint. Your teacher mistakenly wrote
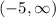`(-5, \infty)` for choice A, when they should have written
`[-5, \infty)`

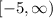
I think either your teacher made a typo or somehow the formatting messed up. Either way, choice A is the closest to the answer.