Question

In an arithmetic progression the sum of the fifth and sixth terms is 44 and the sum of the first eighteen terms is thrice the sum of the first ten terms, find the value of the

Answer 1

a = 5.5, d = 11/3

Explanation:

An arithmetic progression is a sequence of number such that the difference between consecutive numbers is a constant. It is given by:

`a_n=a+(n-1)d\\a_n \ is\ the \ nth\ term, d\ is\ the\ common\ difference\ and\ n \ is\ the \ number\ of\ terms`

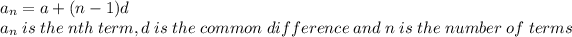
The sum of fifth and sixth terms is 44

Therefore:

a + 4d + a + 5d = 44

2a + 9d = 44 (1)

The sum of the first n terms is:

`S=(n)/(2) (2a+(n-1)d)\\Therefore\ the\ sum\ of\ the\ first\ 18\ term\ is:\\\\S=(18)/(2) (2a+(18-1)d) = 9(2a+17d)=18a+153d\\\\The\ sum\ of\ the\ first\ 10\ term\ is:\\\\S=(10)/(2) (2a+(10-1)d) = 5(2a+9d)=10a+45d`

Since the sum of the first eighteen terms is thrice the sum of the first ten terms:

18a + 153d = 3(10a + 45d)

18 a + 153d = 30a + 135d

18a - 30a + 153d - 135d = 0

-12a + 18d = 0 (2)

Multiply equation 1 by 6 and add to equation 2:

72d = 264

d = 11/3

Putting d = 11/3 in eqn 2

-12a + 18(11/3) = 0

-12a + 66 = 0

12a = 66

a = 5.5