Answer:
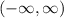
=================================================
Step-by-step explanation:
Draw out a number line. Plot 0 and -4 on the number line.
Shade to the left of x = 0, and have a filled in circle at the endpoint. This is the graph of
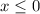
Then graph
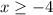 by plotting a filled in circle at -4, and shading to the right.
by plotting a filled in circle at -4, and shading to the right.
Note how the two graphs overlap to cover the entire real number line
So if we have
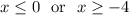 then we're basically saying x is any real number. To write this in interval notation, we write
then we're basically saying x is any real number. To write this in interval notation, we write
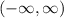
This is the interval from negative infinity to positive infinity (or just infinity). We exclude each endpoint because we can't actually reach infinity itself. Infinity is not a number. Infinity is a concept.
-------------
Side note: if you change the "or" to "and", then the solution to
 would be
would be
![[-4, 0]](https://img.qammunity.org/2021/formulas/mathematics/college/bsxzl475ngf3ibdjwrhrtql8bp8pd6759h.png) to indicate the interval from x = -4 to x = 0, including both endpoints. This is the region where the two graphs overlap.
to indicate the interval from x = -4 to x = 0, including both endpoints. This is the region where the two graphs overlap.