Answer:
The general solution to
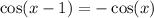 is
is
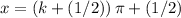 for all integer
for all integer
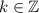 .
.
Explanation:
Given:
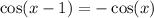 .
.
Rearrange to obtain:
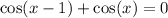 .
.
By sum-of-angle identity for cosines:
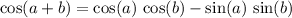 .
.
Since
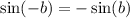 , the following is also an identity:
, the following is also an identity:
 .
.
Add these two identities together to obtain the sum-to-product formula:
 .
.
Simplify to obtain the formula:
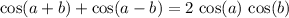 .
.
Before applying this sum-to-product formula to
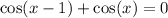 , it would be necessary to find the
, it would be necessary to find the
 and
and
 such that:
such that:
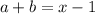 .
.
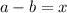 .
.
Solve this system of equations for
 and
and
 to obtain
to obtain
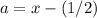 and
and
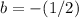 .
.
Apply the sum-to-product formula:
 .
.
In other words, the original equation
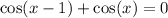 is equivalent to
is equivalent to
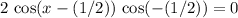 . Solve this new equation for
. Solve this new equation for
 :
:
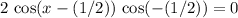 .
.
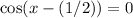 .
.
 .
.
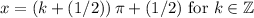 .
.
Therefore, the general solution to
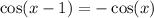 is
is
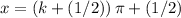 for all
for all
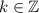 .
.