Question

20 points! Thanks for the help :)

Answer 1

`-2x^6+7x^4+3x^3-3x^2+11x+20`

Explanation:

a) We can expand
`(-2x^3 + x - 5) (x^3 - 3x - 4)`, getting
`-2x^6+6x^4+8x^3+x^4-3x^2-4x-5x^3+15x+20`. We can then combine like terms, getting
`-2x^6+7x^4+3x^3-3x^2+11x+20`.

b) Yes it is the same, as it doesn't matter the order if you multiply two polynomials. It will always be the same.

Answer 2

Explanation:

a) (-2x³ + x - 5)(x³ - 3x - 4)

= (-2x³) (x³ - 3x - 4) + x(x³ - 3x - 4) - 5(x³ - 3x - 4)

= -2x³*x³ - (-2x³)*3x - (-2x³)*4 + x*x³ - x*3x - x*4 + x³ * (-5) - 3x*(-5) -4*(-5)

= -2x⁶ + 6x⁴ + 8x³ + x⁴ - 3x² -4x - 5x³ + 15x + 20 {add like terms}

= -2x⁶ + 6x⁴ + x⁴ + 8x³ - 5x³ - 3x² - 4x + 15x + 20

= -2x⁶ + 7x⁴ + 3x³ - 3x² + 11x + 20

Hint: When multiplying two terms, multiply the coefficient, and add the powers of the variables {
`a^(m)*a^(n)=a^(m+n)` }

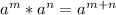-2x³*x³ = (-2*1) *
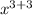`x^(3+3)` = -2x⁶

b) Yes , same because of commutative property of multiplication