Answer:
Explanation:
a) (-2x³ + x - 5)(x³ - 3x - 4)
= (-2x³) (x³ - 3x - 4) + x(x³ - 3x - 4) - 5(x³ - 3x - 4)
= -2x³*x³ - (-2x³)*3x - (-2x³)*4 + x*x³ - x*3x - x*4 + x³ * (-5) - 3x*(-5) -4*(-5)
= -2x⁶ + 6x⁴ + 8x³ + x⁴ - 3x² -4x - 5x³ + 15x + 20 {add like terms}
= -2x⁶ + 6x⁴ + x⁴ + 8x³ - 5x³ - 3x² - 4x + 15x + 20
= -2x⁶ + 7x⁴ + 3x³ - 3x² + 11x + 20
Hint: When multiplying two terms, multiply the coefficient, and add the powers of the variables {
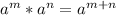 }
}
-2x³*x³ = (-2*1) *
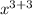 = -2x⁶
= -2x⁶
b) Yes , same because of commutative property of multiplication