Answer:
47.1ft
Explanation:
The find the length of the arc on the quarter circle, we use the following equation:
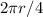
Here,
 is the radius. Just by looking at the diagram, notice how the radius of the quarter circle is equal to the diameter of the semicircles.
is the radius. Just by looking at the diagram, notice how the radius of the quarter circle is equal to the diameter of the semicircles.
Therefore, we substitute 10ft into the equation as
 :
:
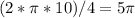
Let's now look at the semicircles. The formula for the length of one of these arcs:
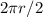
For each semicircle, the diameter is 10ft. We know that the radius is half the length of the diameter, meaning that this time, the radius will be 5ft. Let's substitute that into the equation:
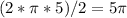
However, here, we have two semicircles, so we multiply this value by 2:
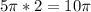
So the final value will be the sum of the length of the arc on the quarter circle and the total length of the arcs of the semicircles:
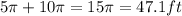 (1dp).
(1dp).
Therefore, to one decimal place, the perimeter of the fountain is 47.1ft.