Question

Calculate the radius of curvatuire of the concave lens based on the measured focal length.

Answer 1

The radius of curvature of the concave lens is 15 centimeters.

To calculate the radius of curvature (R) of a concave lens based on the measured focal length (f), one can use the thin lens formula:
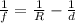`\( (1)/(f) = (1)/(R) - (1)/(d) \)`, where d is the lens-object distance.

Given that the focal length (f) is 15 centimeters, we can rearrange the formula to solve for the radius of curvature (R).

Assuming the object is at a considerable distance (d ≈ ∞ for parallel rays), the equation simplifies to R = -f .

Substituting the given value, the radius of curvature of the concave lens is calculated as R = -15 centimeters.

The negative sign indicates the concave nature of the lens, as the center of curvature is on the same side as the outgoing light.

Therefore, the radius of curvature of the concave lens is 15 centimeters.

The probable question may be:

In a physics experiment conducted in a high school laboratory, a concave lens was used, and its focal length was measured to be 15 centimeters. Calculate the radius of curvature of the concave lens based on the measured focal length

Answer 2

R₁ = (n -1) f

Step-by-step explanation:

In geometric optics the focal length and the radius of curvature are related, for the case of a lens

1 / f = (n₂-n₀) (1 / R₁ - 1 / R₂)

where f is the focal length, n₂ is the refractive index of the material, n₀ is the refractive index of the medium surrounding the material, R₁ and R₂ are the radius of curvature of each of the material's

In our case, the most common is that the lens is in the air, so n1 = 1, in many cases one of the surfaces is flat, so its radius of curvature R₂ = ∞.

1 / f = (n-1) (1 / R₁)

we look for the radius of curvature R₁

1 / R₁ = 1 / f (n-1)

R₁ = (n -1) f

With this expression we can find the radius of curvature of a concave-plane lens