Answer:
The possible values of k are 3 and -3
Explanation:
Given
Points: (-3,k) and (2,0)
Distance between them = √34
Required
Determine the value of k
The distance between two points is calculated as thus;
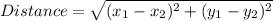
Let
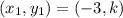
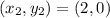
Substitute these values in the given formula
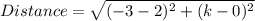
Evaluate the brackets
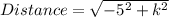
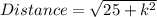
Recall that Distance = √34
So; we have
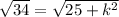
Take square of both sides
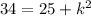
Collect Like Terms
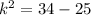
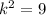
Take square root of both sides
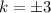
Hence, the possible values of k are 3 and -3