Question

Given the points (–3,k)(–3,k) and (2,0)(2,0), for which values of k would the distance between the points be 34−−√34 ?

Answer 1

The possible values of k are 3 and -3

Explanation:

Given

Points: (-3,k) and (2,0)

Distance between them = √34

Required

Determine the value of k

The distance between two points is calculated as thus;

`Distance = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

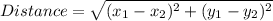
Let

`(x_1,y_1) = (-3,k)`

`(x_2,y_2) = (2,0)`

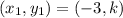
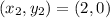
Substitute these values in the given formula

`Distance = √((-3 - 2)^2 + (k - 0)^2)`

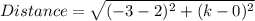
Evaluate the brackets

`Distance = √(-5^2 + k^2)`

`Distance = √(25 + k^2)`

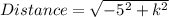
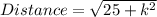
Recall that Distance = √34

So; we have

`√(34) = √(25 + k^2)`

Take square of both sides

`34 = 25 + k^2`

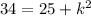
Collect Like Terms

`k^2 = 34 - 25`

`k^2 = 9`

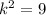
Take square root of both sides

`k = \±3`

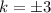
Hence, the possible values of k are 3 and -3