Question

What is the greatest integer a, such that a^2 + 3b is less than (2b)^2, assuming that b is 5? Please answer and have a nice day!

Answer 1

9

Explanation:

I just did the question on AOPS, please see the attachment down below.

Hope this helped! :)

Answer 2

Answer: Largest value is a = 9

===================================================

Work Shown:

b = 5

(2b)^2 = (2*5)^2 = 100

So we want the expression a^2+3b to be less than (2b)^2 = 100

We need to solve a^2 + 3b < 100 which turns into

a^2 + 3b < 100

a^2 + 3(5) < 100

a^2 + 15 < 100

after substituting in b = 5.

------------------

Let's isolate 'a'

a^2 + 15 < 100

a^2 < 100-15

a^2 < 85

a < sqrt(85)

a < 9.2195

'a' is an integer, so we round down to the nearest whole number to get
`a \le 9`

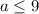
So the greatest integer possible for 'a' is a = 9.

------------------

Check:

plug in a = 9 and b = 5

a^2 + 3b < 100

9^2 + 3(5) < 100

81 + 15 < 100

96 < 100 .... true statement

now try a = 10 and b = 5

a^2 + 3b < 100

10^2 + 3(5) < 100

100 + 15 < 100 ... you can probably already see the issue

115 < 100 ... this is false, so a = 10 doesn't work