Answer: Largest value is a = 9
===================================================
Work Shown:
b = 5
(2b)^2 = (2*5)^2 = 100
So we want the expression a^2+3b to be less than (2b)^2 = 100
We need to solve a^2 + 3b < 100 which turns into
a^2 + 3b < 100
a^2 + 3(5) < 100
a^2 + 15 < 100
after substituting in b = 5.
------------------
Let's isolate 'a'
a^2 + 15 < 100
a^2 < 100-15
a^2 < 85
a < sqrt(85)
a < 9.2195
'a' is an integer, so we round down to the nearest whole number to get
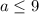
So the greatest integer possible for 'a' is a = 9.
------------------
Check:
plug in a = 9 and b = 5
a^2 + 3b < 100
9^2 + 3(5) < 100
81 + 15 < 100
96 < 100 .... true statement
now try a = 10 and b = 5
a^2 + 3b < 100
10^2 + 3(5) < 100
100 + 15 < 100 ... you can probably already see the issue
115 < 100 ... this is false, so a = 10 doesn't work