Question

The Kelvin temperature of the hot reservoir of an engine is twice that of the cold reservoir, and work done by the engine per cycle is 50 J.

Calculate:
(a) the efficiency of the engine,
(b) the heat absorbed per cycle, and
(c) the heat rejected per cycle.

Answer 1

a) 50%

b) 100 J

c) 50 J

Step-by-step explanation:

The cold temperature of the reservoir =
`T_(c)`

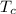
according to the problem, it is stated that the hot reservoir of an engine is twice that of the cold reservoir, therefore,

the hot temperature of the reservoir
`T_(h)` =
`2T_(c)`

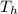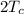
The work done by the engine = 50 J

a) The max efficiency obtainable from a heat engine η =
`1 - (T_(c) )/(T_(h) )`

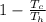
since
`T_(h)` =
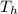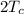`2T_(c)`, the equation becomes

η =
`1 - (T_(c) )/(2T_(c) )` =

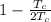η =
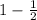`1 - (1 )/(2 )` = 0.5 = 50%

b) The heat absorbed per cycle will be gotten from

η =
`(W)/(Q)`

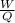
η is the efficiency of the system = 0.5

where W is the work done = 50 J

Q is the heat absorbed = ?

substituting, we have

0.5 =
`(50)/(Q)`

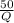
Q = 50/0.5 = 100 J

c) The heat rejected per cycle = 50% of the absorbed heat

==> 0.5 x 100 J = 50 J