Question

Porfabor necesito ayuda en la esta pregunta. ¿Encuentra cuatro pares ordenados de la siguiente función? f(x) = X3 – 2X2 – 2

Answer 1

(0, -2), (1, -3), (2, -2) y (3, 7) son pares ordenados de
`f(x) = x^(3)-2\cdot x^(2)-2`.

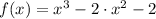Explanation:

Un par ordenado es un elemento de la forma
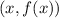`(x,f(x))`, donde
`x` es un elemento del dominio de la función, mientras
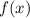`f(x)` es la imagen de la función evaluada en
`x`. Entonces, un par ordenado que está contenido en la citada función debe satisfacer la siguiente condición:

La imagen de la función existe para un elemento dado del dominio. Esto es:

`x \rightarrow f(x)`

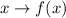
Dado que
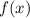`f(x)` es una función polinómica, existe una imagen para todo elemento
`x`. Ahora, se eligen elementos arbitrarios del dominio para determinar sus imágenes respectivas:

x = 0

`f(0) = 0^(3)-2\cdot (0)^(2)-2`

`f(0) = -2`

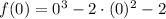
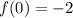
(0, -2) es un par ordenado de
`f(x) = x^(3)-2\cdot x^(2)-2`.

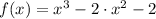x = 1

`f(1) = 1^(3)-2\cdot (1)^(2)-2`

`f(1) = -3`

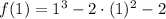
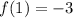
(1, -3) es un par ordenado de
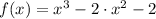`f(x) = x^(3)-2\cdot x^(2)-2`.

x = 2

`f(2) = 2^(3)-2\cdot (2)^(2)-2`

`f(2) = -2`

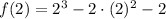
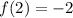
(2, -2) es un par ordenado de
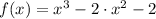`f(x) = x^(3)-2\cdot x^(2)-2`.

x = 3

`f(3) = 3^(3)-2\cdot (3)^(2)-2`

`f(3) = 7`

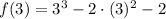
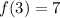
(3, 7) es un par ordenado de
`f(x) = x^(3)-2\cdot x^(2)-2`.

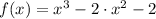(0, -2), (1, -3), (2, -2) y (3, 7) son pares ordenados de
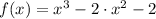`f(x) = x^(3)-2\cdot x^(2)-2`.