Question

Find the mass of the lamina described by the inequalities, given that its density is rho(x, y) = xy. 0 ≤ x ≤ 2, 0 ≤ y ≤ 2

Answer 1

Answer: Mass of lamina = 4

Explanation: A lamina is a plate in 2 dimensions, described by the plane it covers and its density function,
`\rho(x,y)`.

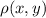To determine mass of the lamina:

mass (M) =
`\int {\int\limits_D \rho(x,y) \, dA`

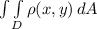
where D is region bounded by the axis.

For the question:

M =
`\int\limits^2_0 {\int\limits^2_0 xy \, dy \,dx`

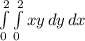
Calculating the double integral:

M =
`\int\limits^2_0 { x(y^(2))/(2) \,dx`

M =
`\int\limits^2_0 { x((2^(2))/(2)-0)} \,dx`

M =
`\int\limits^2_0 { 2x} \,dx`

M =
`(2.2^(2))/(2) - 0`

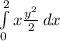
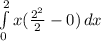
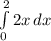
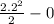
M = 4

The mass of lamina is 4 units.