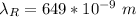Answer:
The wavelength is
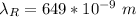
Step-by-step explanation:
From the question we are told that
The wavelength of the red laser is
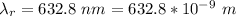
The spacing between the fringe is
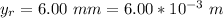
The spacing between the fringe for smaller laser point is
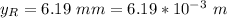
Generally the spacing between the fringe is mathematically represented as
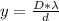
Here
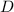 is the distance to the screen
is the distance to the screen
and d is the distance of the slit separation
Now for both laser red light light and small laser point D and d are same for this experiment
So
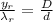
=>
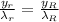
Where
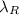 is the wavelength produced by the small laser pointer
is the wavelength produced by the small laser pointer
So
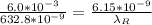
=>