Question

A sealed tank containing seawater to a height of 10.5 mm also contains air above the water at a gauge pressure of 2.95 atmatm. Water flows out from the bottom through a small hole. How fast is this water moving?

Answer 1

C. effusion because there is a movement of a gas through a small opening into a larger volume

Step-by-step explanation:

Edge2020

Have a great day y'all :)

Answer 2

The water is flowing at the rate of 28.04 m/s.

Step-by-step explanation:

Given;

Height of sea water, z₁ = 10.5 m

gauge pressure,
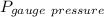`P_(gauge \ pressure)` = 2.95 atm

Atmospheric pressure,
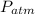`P_(atm)` = 101325 Pa

To determine the speed of the water, apply Bernoulli's equation;

`P_1 + \rho gz_1 + (1)/(2)\rho v_1^2 = P_2 + \rho gz_2 + (1)/(2)\rho v_2^2`

where;

P₁ =
`P_(gauge \ pressure) + P_(atm \ pressure)`

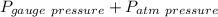
P₂ =
`P_(atm)`

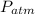
v₁ = 0

z₂ = 0

Substitute in these values and the Bernoulli's equation will reduce to;

`P_1 + \rho gz_1 + (1)/(2)\rho v_1^2 = P_2 + \rho gz_2 + (1)/(2)\rho v_2^2\\\\P_1 + \rho gz_1 + (1)/(2)\rho (0)^2 = P_2 + \rho g(0) + (1)/(2)\rho v_2^2\\\\P_1 + \rho gz_1 = P_2 + (1)/(2)\rho v_2^2\\\\P_(gauge) + P_(atm) + \rho gz_1 = P_(atm) + (1)/(2)\rho v_2^2\\\\P_(gauge) + \rho gz_1 = (1)/(2)\rho v_2^2\\\\v_2^2 = (2(P_(gauge) + \rho gz_1))/(\rho) \\\\v_2 = \sqrt{ (2(P_(gauge) + \rho gz_1))/(\rho) }`

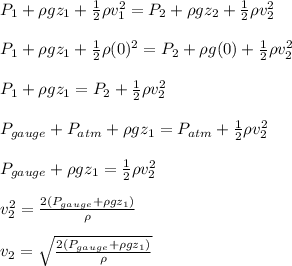
where;

`\rho` is the density of seawater = 1030 kg/m³

`v_2 = \sqrt{ (2(2.95*101325 \ + \ 1030*9.8*10.5 ))/(1030) }\\\\v_2 = 28.04 \ m/s`

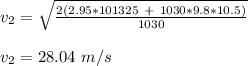
Therefore, the water is flowing at the rate of 28.04 m/s.