Answer:
When x = -4 and y = -6, p = 37.75
Explanation:
Given that p = x² - y²/x² + x·y, we have;
p = (x² × x² -y² + x·y×x²)/x²
p = (x²⁺² - y² + x¹⁺² × y)/x²
p = (x⁴ - y² + x³·y)/x²
Therefore, p in the simplest form is given as follows;
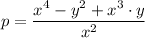
To find the value of p when x = -4 and y = -6, we plug in the value of x and y into the above equation to get the following equation;
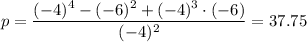
Therefore, the value of p when x = -4 and y = -6 is equal to 37.75.