Question

Enter the correct value so that each expression is a perfect square trinomial

Answer 1

Explanation:

First, let's look at some examples of what a perfect square trinomial looks like.
`x^2 + 16x + 64`

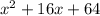
This trinomial is made from:

`(x+8)^2`

So for your second question (x^2 + ___x + 36), we need to work backwards, starting with the last number of the trinomial, 36. Think of two identical numbers that would make 36 if they got multiplied together. Or: √36. Either way, we get 6. So we can put this as a squared binomial.

`(x+6)^2`

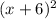
Then, we could solve the binomial to get our middle number. (Use FOIL: Multiply the First terms, then Outer terms, then Inner terms, and Last terms)

`(x+6)(x+6)`

`x^2+6x+6x+36\\x^2+12x+36`

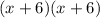
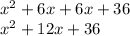
As you can see, our middle number is 12x, and that is what goes into the blank.

Answer: 12x

Answer 2

12x

Explanation:

This is b/2^2, so basically you take the square root of 36 and multiply that value by 2.

so
`√(36)` = 6(2)=12

Hope this makes sense!