Explanation:
First, let's look at some examples of what a perfect square trinomial looks like.
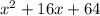
This trinomial is made from:
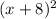
So for your second question (x^2 + ___x + 36), we need to work backwards, starting with the last number of the trinomial, 36. Think of two identical numbers that would make 36 if they got multiplied together. Or: √36. Either way, we get 6. So we can put this as a squared binomial.
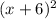
Then, we could solve the binomial to get our middle number. (Use FOIL: Multiply the First terms, then Outer terms, then Inner terms, and Last terms)
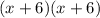
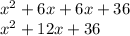
As you can see, our middle number is 12x, and that is what goes into the blank.
Answer: 12x